Data Aggregation: 5 to 30/60 minute

Prior to 2018, the 30- and 60-minute PSM3 data reflected “instantaneous” values for nominal 4 km pixels. Starting in 2018 when higher resolution (5 minute, 2 km) GOES imagery became available, the 30- and 60-minute values switched to being spatial and temporal averages of the higher-resolution 5-minute data.

This notebook recreates the aggregation performed to calculate the 30- and 60-minute values from the 5-minute values.

Starting with the 30-minute values, the spatial average is easy: each 4 km pixel comprises four 2 km pixels, so get data for the four constituent pixels and average them together. The temporal average is slightly complicated in that, because the 30-minute values are symmetrical averages of seven 5-minute values, some 5-minute values contribute to two separate interval averages. Here’s an ASCII illustration of this concept:

Timestamps: 00 05 10 15 20 25 30 35 40 45 50 55 00 05 10 15 20 25
Interval 1:          --------------------
Interval 2:                            --------------------

The 5-minute value at minute 45 gets incorporated into the average for both 30-minute intervals.

Note that this method does not perfectly recreate the 30-minute values, and I’m not sure that this is actually what happens in the real NSRDB. But it does get pretty close.

import pvlib
import matplotlib.pyplot as plt
import pandas as pd

lat, lon = 40.005, -80.005

# Be aware that `get_psm3()` uses a different endpoint for interval=5 than it does for interval=30 or 60

kwargs = dict(latitude=lat, longitude=lon, api_key='DEMO_KEY', email='assessingsolar@gmail.com',
              names='2018', map_variables=False, leap_day=True)

df_4km30, meta = pvlib.iotools.get_psm3(interval=30, **kwargs)
print('4 km pixel coords:', meta['Latitude'], meta['Longitude'])  # 40.01 -80.02

4 km pixel coords: 40.01 -80.02

df_2km1, meta = pvlib.iotools.get_psm3(interval=5, **kwargs)
print('2 km pixel coords:', meta['Latitude'], meta['Longitude'])  # 40.00 -80.01

2 km pixel coords: 40.0 -80.01

So the center of the outer 4 km pixel is North and West of the center of the inner 2 km pixel. That means the other three inner 2km pixels in this 4 km pixel are North, West, and North-West of this one. Since the 2 km pixels are 0.02 degrees on a side, that means stepping 0.02 degrees will get us the neighbor pixels:

kwargs['latitude'] = lat
kwargs['longitude'] = lon - 0.02  # one pixel west
df_2km2, meta = pvlib.iotools.get_psm3(interval=5, **kwargs)
print('2 km pixel coords:', meta['Latitude'], meta['Longitude'])  # 40.00 -80.03

2 km pixel coords: 40.0 -80.03

kwargs['latitude'] = lat + 0.02  # one pixel north
kwargs['longitude'] = lon
df_2km3, meta = pvlib.iotools.get_psm3(interval=5, **kwargs)
print('2 km pixel coords:', meta['Latitude'], meta['Longitude'])  # 40.02 -80.01

2 km pixel coords: 40.02 -80.01

kwargs['latitude'] = lat + 0.02  # one pixel north-west
kwargs['longitude'] = lon - 0.02
df_2km4, meta = pvlib.iotools.get_psm3(interval=5, **kwargs)
print('2 km pixel coords:', meta['Latitude'], meta['Longitude'])  # 40.02 -80.03

2 km pixel coords: 40.02 -80.03

Now, implement the spatiotemporal aggregation method described above. I think this is about as clean as it gets when using pandas, but please let me know if there’s a better way.

def aggregate30(x1, x2, x3, x4):
    avg_5min = pd.concat([x1, x2, x3, x4], axis=1).mean(axis=1)
    resampler = avg_5min.shift(3).resample('30T')
    sum_30min_6samples = resampler.sum()
    avg_30min_7samples = (sum_30min_6samples + resampler.first().shift(-1)) / 7
    return avg_30min_7samples

columns = ['GHI', 'DNI', 'DHI']
fig, axes = plt.subplots(2, len(columns), figsize=(9, 6))

for i, column in enumerate(columns):
    x = df_4km30[column]
    y = aggregate30(df_2km1[column], df_2km2[column], df_2km3[column], df_2km4[column])
    axes[0, i].scatter(x, y, s=1)
    axes[0, i].set_xlabel(f'PSM3 {column} [W/m2]')
    axes[0, i].set_ylabel(f'Calculated {column} [W/m2]')

    axes[1, i].scatter(x, x - y, s=1)
    axes[1, i].set_ylabel(f'{column} Difference (PSM3 $-$ Calculated) [W/m2]')

fig.tight_layout()

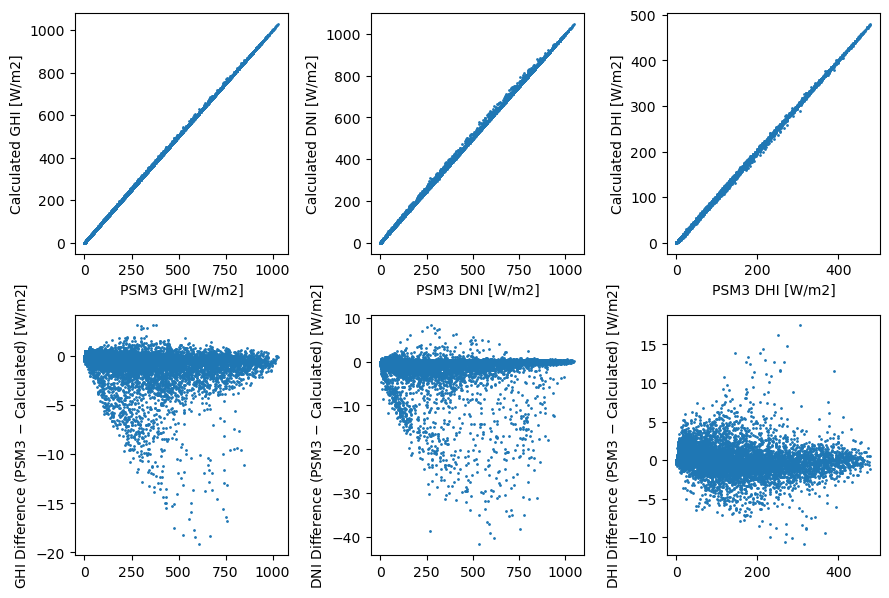
The 60-minute values are dead simple: they’re actually just every other 30-minute value. Therefore, they actually reflect the average only over the 30 minutes centered on the timestamp, not the entire hour. Here’s an ASCII illustrattion:

Timestamps: 10 15 20 25 30 35 40 45 50 55 00 05 10 15 20 25 30 35 40 45 50
Interval 1:    --------------------
Interval 2:                                        --------------------

Other than simplicity and not having to store a separate dataset, it’s not clear to me why this is a good idea – I’d have thought that extending the above approach (average of thirteen 5-minute values) would make more sense.

Regardless, let’s show that it’s true:

df_4km60, meta = pvlib.iotools.get_psm3(interval=60, **kwargs)
print('4km cell coords:', meta['Latitude'], meta['Longitude'])  # 40.01 -80.02

4km cell coords: 40.01 -80.02

columns = ['GHI', 'DNI', 'DHI']
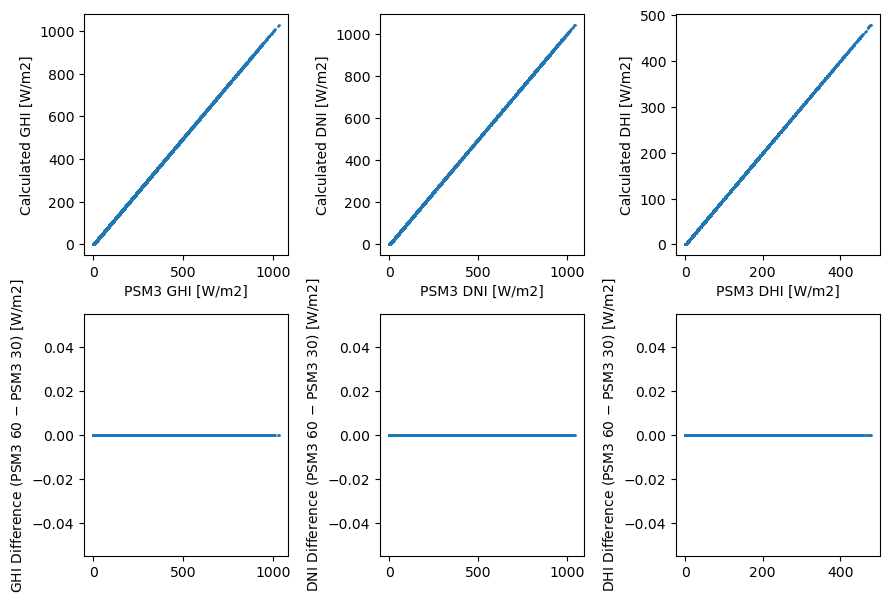
fig, axes = plt.subplots(2, len(columns), figsize=(9, 6))

for i, column in enumerate(columns):
    x = df_4km60[column]
    y = df_4km30[column][1::2]  # take every other 30-minute value
    axes[0, i].scatter(x, y, s=1)
    axes[0, i].set_xlabel(f'PSM3 {column} [W/m2]')
    axes[0, i].set_ylabel(f'Calculated {column} [W/m2]')

    axes[1, i].scatter(x, x - y, s=1)
    axes[1, i].set_ylabel(f'{column} Difference (PSM3 60 $-$ PSM3 30) [W/m2]')

fig.tight_layout()

%load_ext watermark
%watermark --iversions -u -d -t

Last updated: 2022-09-22 21:27:07

pvlib     : 0.9.3
pandas    : 1.5.0
matplotlib: 3.5.2